인공지능 요모조모
[CV] 인공지능 개론(2) 최적화 알고리즘 본문
인공지능 개론(1) https://dvlhyeon248.tistory.com/16
4. 최적화 알고리즘(Model Parameter Optimizer)
▪️딥러닝 모델이 더 나은 예측을 할 수 있도록 가중치를 조정해주는 도구
👉🏻 즉, 모델 학습 과정에서 가중치를 어떻게 효율적으로 조정할 것인지 결정하는 역할
✅ 모델 학습 = 최적화(optimization) 수행
▪️손실 함수의 최솟값을 찾아나가는 일련의 과정
▪️학습률(learning rate): 한 스텝마다 이동하는 보폭
▪️현 지점의 기울기(gradient): 앞으로 이동할 방향
▪️weight의 업데이트 = 에러를 낮추는 방향(decent, (-)부호) x lr x gradient 👉🏻 - γΔF(a^n)
📌 딥러닝 학습 과정 = 눈을 감고 산을 내려가는 것
▪️즉, 산 꼭대기에서 시작해 더 낮은 위치(더 나은 예측)를 찾아가야 함
✅ 가중치(weights) → 현재 우리가 어디에 위치해 있는지 나타냄
✅ 손실(loss) → 우리가 얼마나 높은 곳(잘못된 예측) 에 있는지 나타냄
✅ 옵티마이저(optimizer) → 앞이 보이지 않는 상태에서 더 낮은 곳으로 가는 길을 찾는 역할
📌 산을 내려가는 방법 = 최적화 과정
▪️상황에 따라 큰 보폭(step size ↑) 또는 작은 보폭(step size ↓), 평지/오르막을 거치는 등의 이동방식 결정 필요
▪️신경망은 점진적으로 최적의 해에 수렴하기 위해 여러 최적화 알고리즘(Optimizer)을 사용

✅ Gradient Descent(GD, 경사 하강법)
▪️손실 함수의 기울기를 이용해 최솟값을 찾는 알고리즘
▪️전체 데이터 집합을 이용해 기울기를 계산하고, 파라미터를 업데이트함
👎🏻계산 비용이 큼(데이터 집합 크기에 비례)
1. 방향을 중심으로 하는 Optimizer (gradient 이용)
✅ Stochastic Gradient Descent (SGD, 확률적 경사 하강)

▪️GD의 개선 버전으로, 하나의 샘플을 랜덤하게 선택하여 기울기 계산
👍🏻계산량이 적고 빠름
👎🏻최적 해 주변에서 진동이 심하고, 수렴이 불안정함
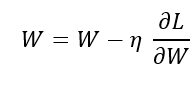
📌 SGD는 랜덤하게 선택한 하나의 데이터 샘플을 사용해서 기울기를 계산
👉🏻각 샘플의 기울기가 다 다름
👉🏻기울어진 방향이 전체 최솟값과 다를 수 있음(샘플에 따라 흔들리며 이동)
👉🏻위의 사진과 같은 지그재그 경로로 이동
여기서 문제는 기울기는 항상 가파른 내리막 방향을 가리킨다는 것
따라서, 손실함수가 축마다 기울기가 다르게 변하는 비등방성(anisotropy) 함수라면 문제가 될 수 있음
- 불안정한 학습
- local minima(지역 최소점), saddle point(안장점)
✅ Momentum(모멘텀)

▪️GD에 관성(momentum) 개념을 추가하여, 빠르게 수렴하도록 개선
▪️이전 업데이트 값을 일정 비율로 유지하면서 현재 기울기를 반영하여 업데이트
👍🏻진동을 줄이고 빠르게 최적값에 도달 가능
👎🏻잘못된 방향으로 가면 빠르게 벗어나기 어려움
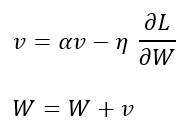
📌v는 속도(velocity)를 나타내며, 기울기가 동일한 부호를 가지면 v의 절댓값은 계속 증가!
👉🏻= v가 증가할수록 x축의 변화폭이 커짐 = 기울기가 변하지 않는 방향으로 가속 → SGD보다 빠르게 수렴🆗
👉🏻기울기가 0이더라도 v값이 더해지면서 멈추지 않고 옆으로 이동 가능 → local minima/saddle point 탈출🆗
✅ Nesterov Accelerated Gradient (NAG, 네스테로프 가속 경사 하강법)
▪️Momentum의 개선 버전으로, 관성을 활용해 더 좋은 방향을 예측하여 업데이트
▪️현재 위치가 아니라, 이동할 위치를 미리 고려하여 기울기를 계산
👍🏻불필요한 진동을 줄이고 더욱 빠르게 수렴

📌일단 관성 방향으로 움직이고, 움직인 자리에 스텝을 계산
👉🏻이전 스텝의 v 방향을 따라 이동한 자리에서 기울기를 계산하여 해당 위치로 실제 이동
👉🏻기울기를 계산하는 지점과 실제 이동하는 지점이 다름
👉🏻이렇게 하면 수식에 error-correction term이라는 이전 v와 현재 v간의 차이를 반영하게 됨 → 급격한 슈팅 방지
2. 보폭을 중심으로 하는 Optimizer (gradient 제곱 이용)
✅ Adagrad (Adaptive Gradient Algorithm)

▪️학습률을 개별 파라미터마다 다르게 조절하여 자주 업데이트되는 가중치는 학습률을 작게, 드물게 업데이트되는 가중치는 학습률을 크게 설정
👍🏻희소한(feature가 드문) 데이터에서도 효과적
👎🏻학습률이 계속 감소하여 나중에는 거의 업데이트되지 않음
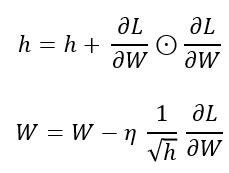
📌신경망 학습에서는 학습률(lr)를 적절하게 설정하는 것이 중요함
👉🏻처음엔 크게 학습하다가 점차 작게 학습하는 방식의 학습률 감소(learning rate decay) 기술 사용
👉🏻이 기술을 발전시킨 것이 AdaGrad
즉, 각 매개변수에 적응적으로 조정하여 맞춤형 lr을 만듦
이때, h를 통해 기울기 제곱에 반비례하도록 학습률을 조정
👉🏻즉, 기울기가 가파를수록 살짝씩 이동하고, 완만할 수록 크게 이동(각 가중치마다 다른 학습률 적용)
👉🏻변동 줄이는 효과🆗
🤔그러나 학습이 진행될 수록 h는 축적됨 → h값이 커질수록 rl은 작아짐 → 기울기가 0인 부근에서 학습이 급격하게 느려져 local minima와 saddle point에 빠질 위험⬆️
* ⊙는 elementwise product
✅ Adadelta
▪️Adagrad의 단점을 개선하여, 학습률이 너무 작아지는 문제를 해결
▪️과거의 기울기 변화량을 누적하여 학습률을 조정
👍🏻학습률을 따로 설정할 필요없음
👎🏻계산량이 많을 수 있음
✅ RMSprop (Root Mean Square Propagation)
▪️Adagrad와 비슷하지만, 기울기의 변화량을 지수 가중 이동 평균으로 계산하여 학습률 감소 문제를 해결
👍🏻과거의 기울기 변화량을 고려하여 학습률을 조절, Adagrad보다 더 효과적
👎🏻적절한 하이퍼파라미터(특히 감쇠 비율)를 찾아야 함
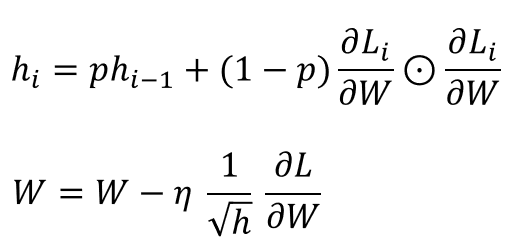
📌Adagrad와 거의 동일하지만, 보폭은 갈수록 줄이되, 이전 기울기 변화의 맥락을 살피자는 부분이 추가
👉🏻h와 기울기 제곱에 각각 p와 (1-p)의 감쇠 비율(decay rate)이 추가됨(보통 0.9 또는 0.99 사용)
👉🏻이전 기울기를 더 크게 반영하여 h가 단순 누적되며 증가하는 것을 방지
= 지수 가중 이동 평균(exponentially weighted moving average)
3. 방향과 보폭을 모두 신경쓰는 Optimizer
✅ Adam (Adaptive Moment Estimation)

▪️모멘텀과 RMSprop을 결합한 알고리즘으로, 1차 및 2차 모멘트를 활용하여 학습률을 조정
👍🏻기본적으로 좋은 성능을 보이며, 많은 문제에서 효과적
👎🏻특정 문제에서는 일반적인 SGD보다 일반화 성능이 떨어질 수도 있음
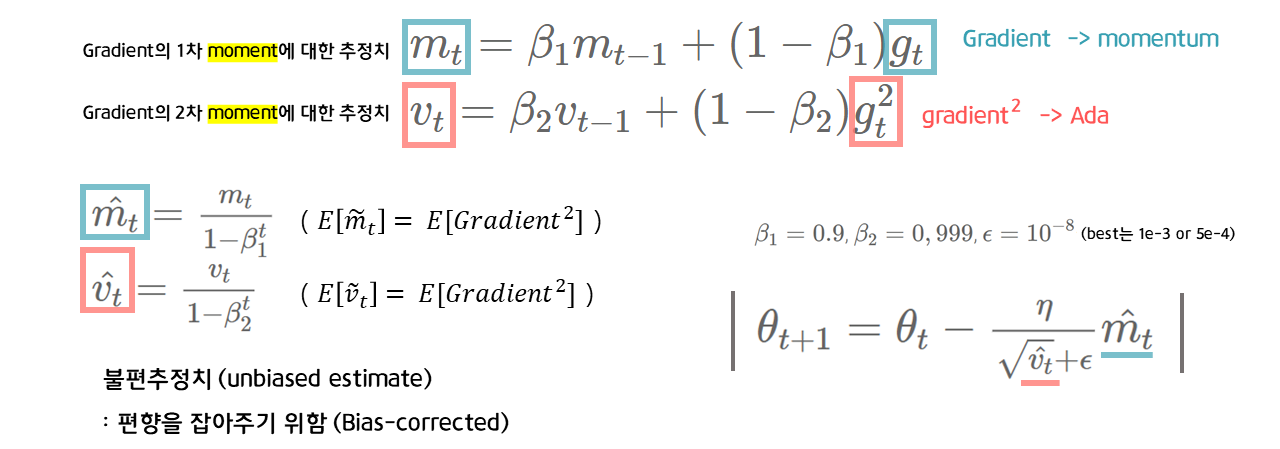
📌방향을 중심으로 한 Momentum 계열과 보폭을 중심으로 한 Ada계열을 결합하여 보폭도, 방향도 적절하게 조절하는 optimizer
👉🏻기울기의 1차 모멘트(moment, 적률 = X의 n차 기댓값)에 대한 추정치 → m 계산
👉🏻기울기의 2차 모멘트에 대한 추정치 → v 계산
+ 불편추정치
⭐ 상황에 맞는 최적화 전략을 선택하는 것이 중요함!
참고:
'ROKEY > Machine Learning' 카테고리의 다른 글
| [CV] 인공지능 개론(4) 선형 회귀(Linear Regression) & 다항 회귀(Polynomial Regression) (0) | 2025.02.27 |
|---|---|
| [CV] 인공지능 개론(3) 목적함수(Objective Function), 손실함수(Loss Function), 비용함수(Cost Function) (0) | 2025.02.26 |
| [CV] 인공지능 개론(1) FC Layer와 MLP (0) | 2025.02.19 |



